De Bruijn Sequence and Universal Cycle Constructions
| Multisets | Output | ||||||||
|
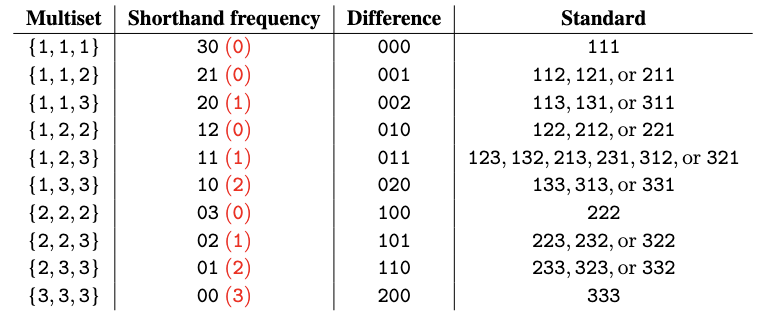
The number of $k$-multisets of $[n]$ = $\{1,2,\ldots, n\}$ is ${n+k-1 \choose k}$. Universal cycles for the $k$-multisets of $[n]$ have been studied by considering a standard string representation, i.e., either 112, 121, or 211 can be used to represent the multiset $\{1,1,2\}$. This representation has a major drawback; UCs exist only if $n$ divides ${n+k-1 \choose k}$ [HGZ09]. Jackson first studied the existence of such sequences when $k=3$ and $k=4$ [Jac93].
Another method to represent a $k$-multiset is with a frequency map, which is a length-$n$ string $f_1f_2\cdots f_n$ where each $f_i$ represents the number of occurrences of $i$ in the multiset. Note, $\sum_{i=1}^n f_i = k$. It is a simple exercise to demonstrate that universal cycles for $k$-multisets do not exist using this representation for $n,k \geq 2$. However, observe that the final symbol $f_n$ in a frequency map is redundant: its value can be determined from the previous $n-1$ values, $f_n = k - \sum_{i=1}^{n-1} f_i$. Thus, we say $f_1\cdots f_{n-1}$ is a shorthand frequency representation for a multiset of $[n]$. Universal cycles always exist and can be efficiently constructed using this represenation [CJS25].
Like with $k$-subsets, a difference representation can be used for $k$-multisets: Assign the first symbol to be the smallest element in the multiset minus one, and assign each successive symbol in the string to be the difference of the next element in the non-dcreasing multiset and the previous element. Universal cycles always exist and can be efficiently constructed using this represenation [CJS25].
These three representations are illustrated in the following table:
UCs for $n=5$ and $k=3$ are given below for the shorthand frequency and difference representations:
- 0011021203 (shorthand frequency)
- 0001011002 (difference)
Shorthand frequency representation
Applying the shorthand frequency representation, each $k$-multiset can be uniquely represented by a string over $\{\tt{0,1},\ldots, \tt{k}\}$ of length $n-1$, where the weight of each string is bounded above by $k$. A universal cycle for such a set of representatives corresponds to a DB sequence with bounded weight. Eight $O(n)$-time successor-rule constructions are provided in [GSWW20] based on the PCR1-PCR4 $k$-ary DB sequence constructions. Concatenation approaches for each algorithm are also given in [SSTW24], where each symbol can be generated in $O(1)$-amortized time. An MSR-based construction is given in [CJS25].
We provide two constructions above that have interesting concatenation properties. The generalized Grandmama visits necklaces of length $m$ with weight at most $w$ as they appear in colex order. The MSR-based construction visits necklaces of length $m+1$ with weight exactly $w$ as they appear in reverse colex order. Examples below are for $k$-multisets where $k=4$ and $n=4$: $$ \mbox{Grandmama} = \tt{0 \cdot 001 \cdot 011 \cdot 1 \cdot 021 \cdot 031 \cdot 002 \cdot 012 \cdot 112 \cdot 022 \cdot 003 \cdot 013 \cdot 004},$$ $$ \mbox{MSR-based} = \tt{0004 \cdot 0013 \cdot 0103 \cdot 0022 \cdot 0112 \cdot 02 \cdot 0031\cdot 0121 \cdot 0211 \cdot 1.}~~~~~ $$
Difference representation
By applying the difference representation, the set of $k$-multisets corresponds to all strings over the alphabet $\{\tt{0,1,\ldots, n{-}1}\}$ of length $k$, where the weight of each string is bounded above by $n-1$. Like the shorthand frequencey representation, a UC for $k$-multisets using the difference representation is equivalent to a DB sequence with bounded weight [CJS25]. Examples below are for $k$-multisets where $k=4$ and $n=4$: $$ \mbox{Grandmama} = \tt{0 \cdot 0001 \cdot 01 \cdot 0011 \cdot 0111 \cdot 0021 \cdot 0002 \cdot 0102 \cdot 0012 \cdot 0003}, $$ $$ \mbox{MSR-based} = \tt{00003 \cdot 00012 \cdot 00102 \cdot 00021 \cdot 00111 \cdot 01011 \cdot 00201.}~~~~~$$