De Bruijn Sequence and Universal Cycle Constructions
| Universal Cycles for Weak Orders | Output | ||||||
|
A weak order is a way $n$ competitors can rank in an event, where ties are allowed. For example, the times for the 100m men's butterfly final in the 2016 Summer Olympics were:
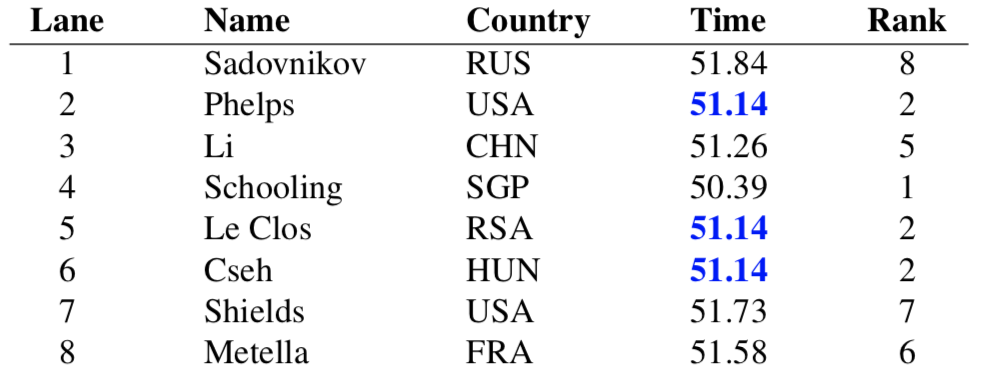
The result was a three way tie for the silver medal. No bronze was awarded. This outcome corresponds to the weak ordering 82512276. Let $\mathbf{W_r}(n)$ denote the set of weak orders (based on this rank representation) in a competition with $n$ competitors (teams). For example, when $n=3$, the 13 different weak orders are \[ \mathbf{W}(3) = \{111, 113, 131, 311, 122, 212, 221, 123, 132, 213, 231, 312, 321\}.\] The number of weak orders of order $n$ are also known as the the ordered Bell numbers or Fubini numbers and their enumeration sequence is A000670 in the Online Encyclopedia of Integer Sequences. The first six terms in this sequence starting at $n=1$ are 1, 3, 13, 75, 541, and 4683 respectively.
The existence of universal cycles for $\mathbf{W}(n)$ was proved in [LG10] using the terminology ranked permutations. For example, 1113213122123 is a UC for $\mathbf{W}(3)$. Using an alternate representation (described below), existence was proved using standard graph techniques in [HH13]. The more difficult problem of efficiently constructing universal cycles for weak orders was posed in Problem 477 of [JSH09]. Constructions (available for download as C program) for both representations are given in [SW20] based on the framework from [GSSW20].
Height representation
A weak order can be thought of as a binary relation $\preceq$ on $\Sigma = \{1, 2, \cdots, n\}$ that is transitive and complete (or connex). The latter property means that $x \preceq y$ or $y \preceq x$ (or both) for each $x,y \in \Sigma$. We write $x \equiv y$ if $x \preceq y$ and $y \preceq x$, and we write $x \prec y$ if $x \preceq y$ but $y \npreceq x$. Using this notation, a weak order can be written as a permutation where consecutive elements are separated by either $\equiv$ or $\prec$. For example, \[4 \prec 2\equiv 5 \equiv 6 \prec 3 \prec 8 \prec 7 \prec 1\] corresponds to the weak ordering from our earlier example.
The height of element $j$ is defined as the number of $\prec$ symbols that precede $j$ in the weak order. By replacing each element $j$ by its height, the weak order above can be represented by 51201143. Let $\mathbf{W_h}(n)$ denote the set of all weak orders of order $n$ using this height string representation. This is the representation used in [DG08,HH13,JSH09]. As an example, \[ \mathbf{W_h}(3) = \{000, 001, 010, 100, 011, 101, 110, 012, 120, 201, 021, 210, 102\}.\]
The rank of element $j$ is defined as one plus the number of elements that precede the rightmost $\prec$ symbol to the left of $j$ in the weak order. Thus, perhaps more naturally, we can list each competitor $j$ by its rank, as done in [LG10]. Using the rank representation we obtain the string 82512276 as presented in our initial example.
Shift rules for height representation
Using the PCR as the underlying feedback function, the following UC-successors for $\mathbf{W_h}(n)$ are obtained in [SW20], where $\omega = w_1\cdots w_n \in \mathbf{W_h}(n)$, $\omega' = (w_1{+}1)w_2\cdots w_n$, $\omega'' = (w_1{+}2)w_2\cdots w_n$, and $\omega^{-} = (w_1{-}1)w_2\cdots w_n$. The set $\mathbf{R}(n)$ contains each string in $\mathbf{W_h}(n)$ that is the lexicographically largest amongst all its rotations.
$f(\omega) = \left\{ \begin{array}{ll} w_1-1 &\ \ \mbox{if $\omega \in \mathbf{R}(n)$;}\\ w_1+1 &\ \ \mbox{if $\omega \notin \mathbf{R}(n)$ and $\omega'\in \mathbf{R}(n)$ and $\omega'' \notin \mathbf{R}(n)$;}\\ w_1+2 &\ \ \mbox{if $\omega \notin \mathbf{R}(n)$ and $\omega'\in \mathbf{R}(n)$ and $\omega'' \in \mathbf{R}(n)$;}\\ w_1 \ &\ \ \mbox{otherwise.}\end{array} \right.$
$f(\omega) = \left\{ \begin{array}{ll} w_1+1 &\ \ \mbox{if $\omega' \in \mathbf{R}(n)$;}\\ w_1-1 &\ \ \mbox{if $\omega' \notin \mathbf{R}(n)$ and $\omega \in \mathbf{R}(n)$ and $\omega^- \notin \mathbf{R}(n)$;}\\ w_1-2 &\ \ \mbox{if $\omega' \notin \mathbf{R}(n)$ and $\omega \in \mathbf{R}(n)$ and $\omega^- \in \mathbf{R}(n)$;}\\ w_1 \ &\ \ \mbox{otherwise.}\end{array} \right.$
- [DG08] P. Diaconis and R. L. Graham. Products of universal cycles, in A Lifetime of Puzzles. E. Demaine, M. Demaine and T. Rodgers, eds., A K Peters/CRC Press, pages 35– 55, 2008.
- [GSWW20] D. Gabric, J. Sawada, A. Williams, and D. Wong. A successor rule framework for constructing $k$-ary de Bruijn sequences and universal cycles. IEEE Transactions on Information Theory, 66(1):679–687, 2020.
- [HH13] V. Horan and G. Hurlbert. Universal cycles for weak orders. SIAM J. Discrete Math., 27(3):1360-1371, 2013.
- [JSH09] B. Jackson, B. Stevens, and G. Hurlbert. Research problems on Gray codes and universal cycles. Discrete Mathematics, 309(17):5341-5348, 2009.
- [LG10] A. Leitner and A. Godbole. Universal cycles of classes of restricted words. Discrete Mathematics, 310(23):3303-3309, 2010.
- [SW20] J. Sawada and D. Wong. Efficient universal cycle constructions for weak orders. Discrete Mathematics, 343(10):112022, 2020.