De Bruijn Sequence and Universal Cycle Constructions

Euler Cycle Output
Order $n$
Symbols $k$
A graph model and Euler cycles

Given an alphabet of size $k$, the de Bruijn graph of order $n$ is the directed graph $G(n,k) = (V,E)$ where $V$ is the set of all $k$-ary strings of length $n$ and there is a directed edge $e=(u,v)$ from $u = u_1u_2\cdots u_n$ to $v=v_1v_2\cdots v_n$ if $u_2\cdots u_n = v_1\cdots v_{n-1}$. Each edge $e$ is labeled by $v_n$. Outputting the edge labels in a Hamilton cycle of $G(n,k)$ produces a DB sequence. Below (left) is a Hamilton cycle in the de Bruijn graph $G(3,2)$. Starting from 000, its corresponding DB sequence is 10111000.

                                

Each de Bruijn graph is connected and the in-degree and the out-degree of each vertex is $k$; the graph $G(n,k)$ is Eulerian. $G(n,k)$ is the line graph of $G(n{-}1,k)$ which means an Euler cycle in $G(n{-}1,k)$ corresponds to a Hamilton cycle in $G(n,k)$. Thus, the sequence of edge labels visited in an Euler cycle is a DB sequence. Illustrated above (right) is an Euler cycle in $G(3,2)$. The corresponding DB sequence is 0111101011001000.

Finding an Euler cycle in an Eulerian graph is linear-time solvable with respect to the size of the graph. However, since the graph must be stored, applying such an algorithm to find a DB sequence requires exponential $O(k^n)$ space and there is an exponential time delay before the sequence can be output.

Finding an Euler cycle

The following algorithm for finding an Euler cycle is based on Fleury [Fle83] with details taken from [Rus03]. The basic idea is do not burn bridges. In other words, do not visit (and use up) an edge if it leaves the remaining graph disconnected.

Fleury's Euler cycle algorithm (do not burn bridges)
  1. Pick a root vertex and compute a spanning in-tree (arborescence) $T$
  2. Make each edge of $T$ (the bridges) the last edge on the adjacency list of the corresponding vertex
  3. Starting from the root, traverse edges in a DFS manner by visiting the first unused edge in the current vertex's adjacency list
This algorithm is the basis for all the greedy DB constructions as outlined below. Finding a spanning in-tree can be done by reversing the direction of the edges in the Eulerian graph and computing a spanning out-tree with a standard DFS on the resulting graph. The corresponding edges in the original graph will be a spanning in-tree. Using this approach, all binary DB sequences can be generated by considering all possible spanning in-trees. When $k>2$, all possible orderings of the remaining $k-1$ vertices on each adjacency list must also be considered. The BEST Theorem [Fre82] applies this approach to determine the total number of $k$-ary DB sequences of order $n$ is: $$\frac{(k!)^{k^{n-1}}}{k^n}.$$ A C implementation that finds one spanning in-tree to construct a DB sequence is available for download. The next section illustrates three spanning in-trees in $G(3,2)$ for three greedy DB constructions.

A second well-known Euler cycle algorithm is from Hierholzer [Hie73]:

Hierholzer's Euler cycle algorithm (cycle joining)
  1. Start at an arbitrary vertex $v$ visiting edges in a depth-first manner until returning to $v$
  2. Repeat until all edges are visited: Start from any vertex $u$ on the current cycle and visit the remaining edges in a DFS manner until returning to $u$. Join the two cycles together.

This cycle-joining approach is the basis for all the successor rule constructions.

The lexicographically smallest Euler cycle can be generated by applying the ideas of cycle joining [MM09].

Greedy algorithms, preference tables, and Euler cycles

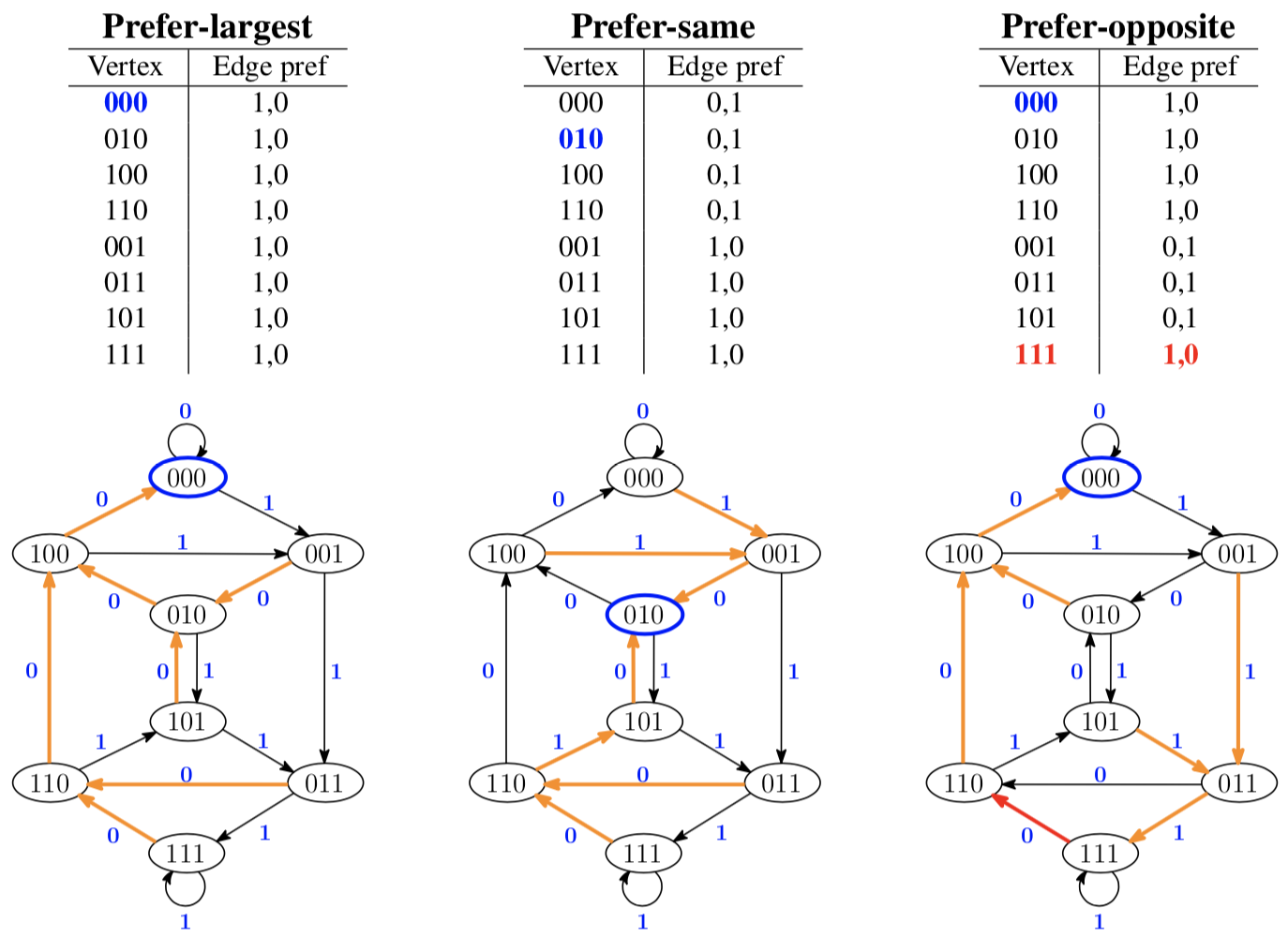
Preference tables [Alh12] (also called look-up tables [Xie87]) generalize the notion of the greedy constructions. In particular, a preference table specifies the precise order in which edges are visited for each vertex when performing Step 3 in Fleury's Euler cycle algorithm. Thus given a preference table and a root vertex, Step 3 in the algorithm can be applied to construct a DB sequence if combining the last edge from each non-root vertex forms a spanning in-tree to the root. For example, the preference tables and corresponding spanning in-trees for the Prefer-largest, Prefer-same, and Prefer-opposite constructions are given below for $G(3,2)$. For the Prefer-largest, the only valid root is 000. For the Prefer-same, either 010 or 101 could be chosen as root. The Prefer-opposite has a small nuance. By its strict definition, the edges will not create a spanning in-tree for any root. But by changing the preference for the single string 111, a spanning in-tree is created when rooted at 000.

          

Download source code

» C program

References

  • [Alh12] A. Alhakim. Spans of preference functions for de Bruijn sequences. Discrete Appl. Math., 160(7-8):992–998, 2012.

  • [Fle83] Fleury. Deux problemes de geometrie de situation. Journal de mathematiques elementaires, 42:257–261, 1883.

  • [Fre82] H. Fredricksen. A survey of full length nonlinear shift register cycle algorithms. Siam Review, 24(2):195–221, 1982.

  • [Hie73] C. Hierholzer. Ueber die Möglichkeit, einen Linienzug ohne Wiederholung und ohne Unterbrechung zu umfahren. Mathematische Annalen, 6:30–32, 1873.

  • [MM09] M. Matamala and E. Moreno. Minimum Eulerian circuits and minimum de Bruijn sequences. Discrete Math., 309(17):5298–5304, 2009.

  • [Rus03] F. Ruskey. Combinatorial generation. Working Version (1j-CSC 425/520), 2003.

  • [Xie87] S. Xie. Notes on de Bruijn sequences. Discrete Appl. Math., 16(2):157-177, 1987.

Interested in generating other combinatorial objects? Visit http://combos.org