De Bruijn Sequence and Universal Cycle Constructions
| Orientable Sequences | Output | ||||||||
|
An orientable sequence is a universal cycle of order $n$ for a set $\mathbf{S}$ that does not contain both a string and its reversal, i.e., if $\mathbf{S}$ contains $w_1w_2\cdots w_n$ then it does not contain its reversal $w_n\cdots w_2w_1$ [DMRW93,MW22]. Thus, $\mathbf{S}$ necessarily excludes palindromes. Orientable sequences find application in robotic position-location systems allowing a robot to determine both its location and orientation. A maximal length orientable sequence for $n=5$ is 001101; they do not exist for $n<5$.
By applying cycle joining, binary orientable sequences of asymptocially optimal length $$ L_n = \left( 2^{n-1} - \frac{1}{2} \sum_{d | n} \mu(n/d) \frac{n}{d} H(d) \right), \ \mbox{where $H(d) = \frac{1}{2} \sum_{i | d} i \left( 2^{\lfloor \frac{i+1}{2} \rfloor} + 2^{\lfloor \frac{i}{2} \rfloor +1} \right)$, }$$ can be efficiently constructed [DMRW93,GS23]. By applying a search starting with these sequences, orientable sequences of length $L^*_n$ have been found as indicated in the table below. Lempel's lift can be applied to recursively construct orientable sequences with length $R_n$ (starting from an orientable sequence of length $R_8=80$ for $n=8$) that is at least 63% of a trivial upper bound $2^{n-1} - 2^{\lfloor (n-1)/2\rfloor}$ [MW22]; a tighter bound $U_n$ is given in the table below [DMRW93].
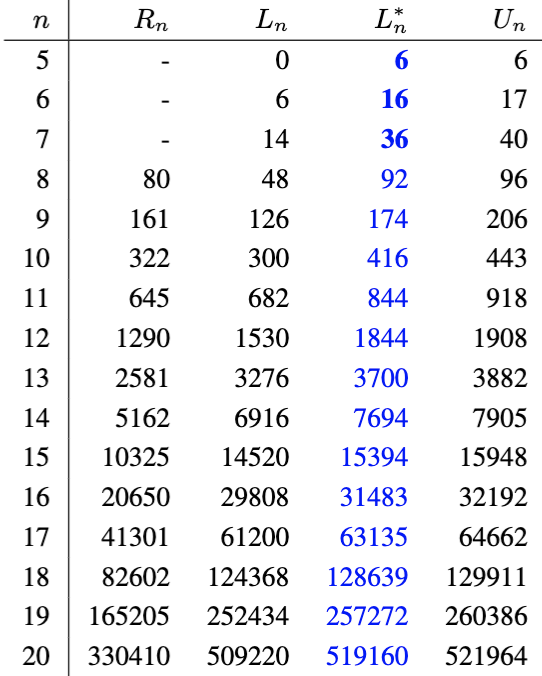
The maximum length of an orientable sequence is known only for $n \leq 7$. The following construction can be generalized to a non-binary alphabet [GS24] with implementations available for download.
Cycle joining and concatenation tree
Let $\mathbf{B}(n)$ denote the set of binary strings of length $n$. The PCR partitions $\mathbf{B}(n)$ into cycles corresponding to equivalence classes of strings under rotation. A cycle can be represented by a necklace, which is the lexicographically smallest string in the corresponding class. If a necklace and its reversal belong to the same cycle, we say it is symmetric; otherwise, it is asymmetric. The following table illustrates the 60 necklaces of length $n=9$, where each asymmetric necklace pair corresponds to a necklace and the necklace of its reversal:
A bracelet is the smallest string in an equivalence class of strings under rotation and reversal; they correspond to the symmetric necklaces together with the smaller of the two asymmetric necklace pairs in the table above. By cycle joining the (highlighted) asymmetric bracelets, an orientable sequence can be constructed of length $L_n$.
Let $\alpha$ denote an asymmetric bracelet not equal to the root node $0^{n-4}1011$. Let $\mathrm{first1}(\alpha)$ denote the necklace obtained by flipping the first 1 in $\alpha$, $\mathrm{last1}(\alpha)$ denote the necklace representative of the string obtained by flipping the last 1 in $\alpha$, and $\mathrm{last0}(\alpha)$ denote the necklace obtained by flipping the last 0 in $\alpha$. Then $$\mathrm{parent}(\alpha) = \left\{ \begin{array}{ll} \mathrm{first1}(\alpha) & \ \ \mbox{if $\mathrm{first1}(\alpha)$ is an asymmetric bracelet;}\\ \mathrm{last1}(\alpha) & \ \ \mbox{if $\mathrm{first1}(\alpha)$ is not an asymmetric bracelet and $\mathrm{last1}(\alpha)$ is an asymmetric bracelet; }\\ \mathrm{last0}(\alpha) \ &\ \ \mbox{otherwise.}\end{array} \right.$$
The cycle-joining tree for $n=9$ (above left) can be converted to a corresponding concatenation tree (above right), which allows each symbol in the corresponding orientable sequence to be generated in $O(1)$-amortized time [SG23]. Outputting the aperiodic prefix (the shortest string $\beta$ such that $\alpha = \beta^t$ for some $t\geq 1$) of each node $\alpha$ in the concatenation tree as they appear in RCL (right-current-left) order produces the following orientable sequence for $n=9$ of length $L_9 = 126$:
$~~~~000001011~
111001011~
011001011~
110011011~
110001011~
100101011~
100011011~
$
$~~~~101011011~
100001001~
110001001~
010001001~
100001011~
001001011~
000101011~
.$
Recursive construction (Lempel's lift)
Let $\mathcal{O}_n$ denote an orientable sequence of order $n$ and length $m$ with odd weight and the following property: it has exactly one substring $0^{n-4}$. Let $\mathcal{O}_{n+1}$ denote the string in $\mathcal{L}(\mathcal{O_n})$ replacing the unique substring $1^{n+1-4}$ with $1^{n+1-3}$ when its weight is even. The resulting orientable sequence has length $2m$ or $2m{+}1$, has odd weight, and has the property of having exactly one substring $0^{n+1-4}$.
Let $\mathcal{O}_6 = \underline{00}1010111$. Then applying $\mathcal{L}$ yields $\mathcal{O}_7 = \underline{000}110010111001101$ which has odd weight. Applying $\mathcal{L}$ again yields 000010001101000100111101110010111011 which has even weight so the unique substring 1111 is replaced with 11111 to yield $$\mathcal{O}_8 = \underline{0000}100011010001001111101110010111011.$$
The implementation used above applies an orientable sequence of order $n=8$ of length 80 as a base case for recursively computing larger orders.
Acyclic orientable sequences
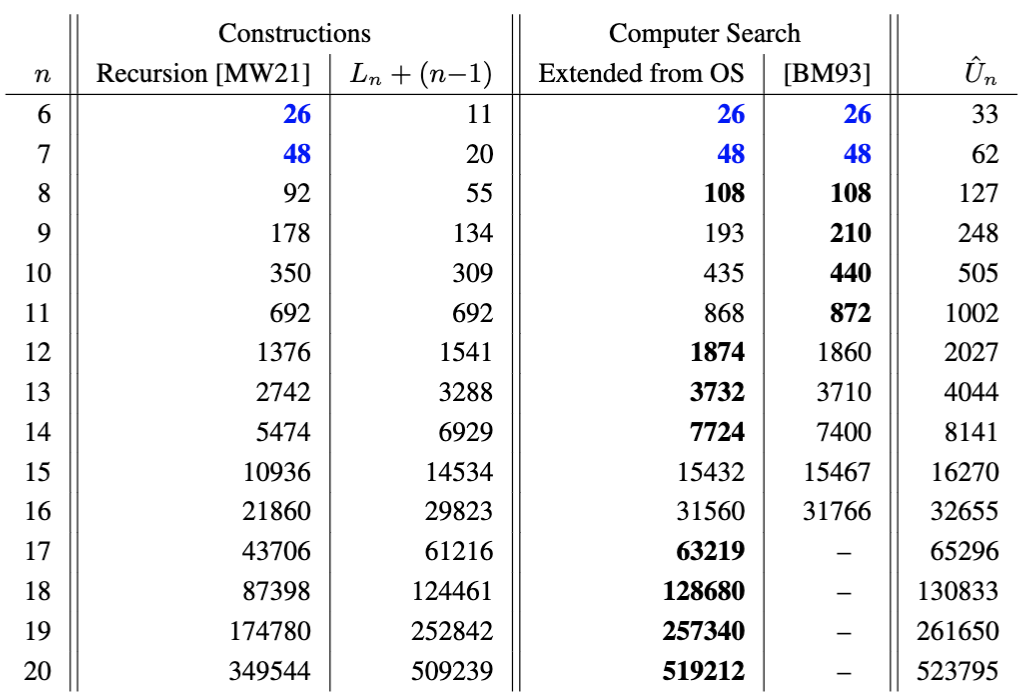
The linear relative of an orientable sequence is known as an acyclic orientable sequence (or aperiodic 2-orientable window sequence in [BM93]). Trivially, they can be obtained from an orientable sequence by copying the length $n{-}1$ prefix and appending it to the end, and a trivial upper bound for their maximal length is $\hat U_n = 2^{n-1} - 2^{\lfloor (n-1)/2\rfloor} + (n{-}1)$. Acyclic orientable sequences that have length at least 2/3 optimal can be constructed by applying properties of Lempel's lift [MW22].
Let $\mathcal{A}_n$ denote an acyclic orientable sequence of order $n$ and length $m$ with the following property: it begins with $0^{n-1}$ and ends with $1^{n-1}$. Let $\mathcal{L}(\mathcal{A_n}) = \{\mathcal{U},\overline{\mathcal{U}} \}$, where $\mathcal{U}$ begins with 0. Construct $\mathcal{A}_{n+1}$ by joining $\mathcal{U}$ with the reversal of $\overline{\mathcal{U}}$ overlapping the alternating suffix of the former with the alternating prefix of the latter. When $n$ is even, the overlap has length $n$; when $n$ is odd, the overlap has length $n{-}1$. $\mathcal{A}_{n+1}$ retains the property of beginning with $0^n$ and ending with $1^n$.
Let $\mathcal{A}_3 = 0011$. $\mathcal{L}(0011) = \{00010, 11101\}$ and $\mathcal{A}_4 = 000\underline{10}111$, where the overlap is underlined. Continuing, $\mathcal{L}(00010111) = \{000011010, 111100101\}$ and $\mathcal{A}_5 = 00001\underline{1010}01111$.
The table below shows the lengths obtained from this recursive construction compared to those that can be constructed by trivially extending the orientable sequences obtained via cycle-joining; it also shows the lengths of the longest known acyclic orientable sequences (the sequences can be dowloaded here) from searches seeded with an orientable sequence of length $L_n^*$, and those discovered by computer search [BM93].
» Binary concatenation C program
» $k$-ary concatenation C program
» Binary successor rule C program
- [BM93] J. Burns and C. J. Mitchell. Position sensing coding schemes, Cryptography and Coding III (M.J. Ganley, ed.), Oxford University Press, Oxford, 1993, pp. 31-66.
- [DMRW93] Z.-D. Dai, K. M. Martin, M. J. B. Robshaw, and P. R. Wild. Orientable sequences, Cryptography and Coding III (M.J. Ganley, ed.), Oxford University Press, Oxford, 1993, pp. 97–115.
- [GS23] D. Gabric and J. Sawada. Efficient construction of long orientable sequences. arXiv preprint arXiv:2108.03069, 2023.
- [GS24] D. Gabric and J. Sawada. Orientable sequences over a non-binary alphabet. Manuscript, 2024.
- [MW22] C. J. Mitchell and P. R. Wild. Constructing orientable sequences. IEEE Transactions on Information Theory, 68(7):4782–4789, 2022.