De Bruijn Sequence and Universal Cycle Constructions

Subsets Output
Algorithm
Order $n$
Subset size $k$
Subsets

Universal cycles for the $k$-subsets of $\{1,2,\ldots, n\}$ have been generally studied by considering a standard string representation, i.e., either 13 or 31 can be used to represent the subset $\{1,3\}$ [CDG92]. This representation has a major drawback; UCs exist only if $n$ divides $n \choose k$. Another common representation for a $k$-subset is a length-$n$ binary string with weight (the number of ones) $k$. It is straightforward to observe that non-trivial UCs do not exist using this representation (see [BG11,RSW12]). However, like permutations, and multiset permutations, by applying a shorthand binary string representation for $k$-subsets (one that omits the final redundant symbol), UCs exist where each subset corresponds to a unique length $n{-}1$ substring with weight $k{-}1$ or $k$ [RSW12]. UCs for $k$-subsets also exist by applying a difference representation, where the first symbol is the smallest element of the subset, and each successive symbol is added to the previous symbol to obtain the next symbol in the subset. These three representations are illustrated in the following table:

     

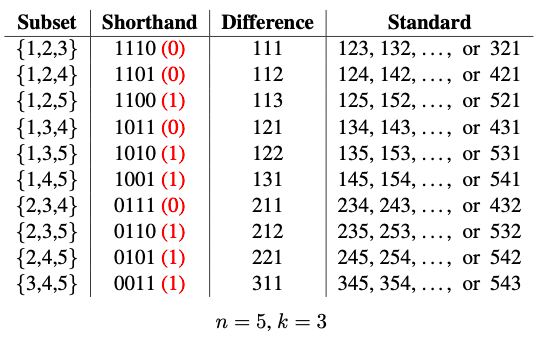
UCs for $n=5$ and $k=3$ are given below for the shorthand and difference representations:

  • 1101011100 (shorthand)
  • 1113112212 (difference)
No UCs exist using the standard representation when $k=n{-}2$ [SBE+02]. When $n=5$ and $k=2$, 1234524135 is a universal cycle using the standard representation. More details about each representation is given below.

Shorthand binary string representation

Applying the shorthand binary string representation, each $k$-subset can be uniquely represented by a binary string of length $n$ and weight (number of 1s) $k$ or $k-1$. Amazingly, a UC for such a set can be obtained by concatenating together the aperiodic prefixes of necklaces with length $n$ and weight $k$ as they appear in reverse cool-lex order [RSW12]. For example, when $n=7$ and $k=3$, the necklaces are $\{0000111, 0001011, 0001101, 0010011, 0010101 \}$ and the following is a reverse cool-lex ordering of these necklaces: $$1100100~1101000~1010100~1011000~1110000.$$ This construction leads to an algorithm that outputs each symbol in $O(1)$-amortized time using $O(n \log n)$ space [SW13]. The sequence can also be generated by an $O(n)$-time successor rule based on the Missing Symbol Register (MSR) which, in the binary case, is equivalent to the PSR/CSR depending on the parity [SW23]. UCs based on the PSR/CSR are also considered in [EL84].

By applying the algorithm in [MM09], the lexicographically smallest UC can be constructed; however, it requires exponential space and delay. An implementation of this algorithm is available for download.

Difference representation

By applying the difference representation, each $k$-subset corresponds to a unique string of length $k$ over an alphabet $\{1,2,\ldots, n-k+1\}$, where the sum of the elements in each string is bounded above by $n$. Thus, a UC for subsets using this representation is equivalent to a DB sequence with bounded weight. Eight $O(n)$-time successor-rule constructions are provided in [GSWW20] based on the PCR1-PCR4 $k$-ary DB sequence constructions. Concatenation approaches for each algorithm are also given in [SSTW24], where each symbol can be generated in $O(1)$-amortized time. DB sequences with bounded weight are also considered in [SWW13].

Standard representation

The standard representation has an immediate drawback, there is a necessary condition that $n$ must divide $n \choose k$ for a UC to exist. Given this constraint, UCs are known to exist for $k=3$ and $k=4$ (implementations based on the existence proof are available for download) [Jac93,Hur94], and that they do not exist for $k=n-2$ [SBE+02]; they are also known to exist if $k$ is fixed, and $n$ is sufficiently large [GJKO20]. This has given rise to the study of subset packings and coverings [CHHM09,DL16]. The standard string representation for subsets has also been considered in [JSH09,Lan12,Rud13].

Download source code

» Cool-lex C program

» Lex min C program

» Difference C program

» Standard C program

References

  • [BG11] A. Blanca and A. P. Godbole. On universal cycles for new classes of combinatorial structures. SIAM Journal on Discrete Mathematics, 25(4):1832–1842, 2011.

  • [CDG92] F. Chung, P. Diaconis, and R. Graham. Universal cycles for combinatorial structures. Discrete Mathematics, 110(1):43–59, 1992.

  • [CHHM09] D. Curtis, T. Hines, G. Hurlbert, and T. Moyer. Near-universal cycles for subsets exist. SIAM Journal on Discrete Mathematics, 23(3):1441–9, 2009.

  • [DL16] M. Debski and Z. Lonc. Universal cycle packings and coverings for $k$-subsets of an $n$-set. Graphs and Combinatorics, 32(6):2323–2337, Nov 2016.

  • [EL84] T. Etzion and A. Lempel. Algorithms for the generation of full-length shift-register sequences. IEEE Trans. Inform. Theory, 30(3):480–484, 1984.

  • [GSWW20] D. Gabric, J. Sawada, A. Williams, and D. Wong. A successor rule framework for constructing $k$-ary de Bruijn sequences and universal cycles. IEEE Transactions on Information Theory, 66(1):679–687, 2020.

  • [GJKO20] S. Glock, F. Joos, D. K\"{u}hn, and D. Osthus. Euler tours in hypergraphs. Combinatorica, 40(5):679–690, November 2020.

  • [Hur94] G. Hurlbert. On universal cycles for $k$-subsets of an $n$-set. SIAM Journal on Discrete Mathematics, 7(4):598–604, 1994.

  • [Jac93] B. W. Jackson. Universal cycles of $k$-subsets and $k$-permutations. Discrete mathematics, 117(1):141–150, 1993.

  • [JSH09] B. Jackson, B. Stevens, and G. Hurlbert. Research problems on Gray codes and universal cycles. Discrete Mathematics, 309(17):5341–5348, 2009.

  • [Lan12] M. Lanius. Universal Cycles for $k$-subsets of an $n$-set. Honors thesis, Wellesley College, 2012.

  • [MM09] M. Matamala and E. Moreno. Minimum Eulerian circuits and minimum de Bruijn sequences. Discrete Math., 309(17):5298–5304, 2009.

  • [Rud13] Y. Rudoy. An inductive approach to constructing universal cycles on the $k$-subsets of $[n]$. The Electronic Journal of Combinatorics, 20:P18, 2013.

  • [RSW12] F. Ruskey, J. Sawada, and A. Williams. De Bruijn sequences for fixed-weight binary strings. SIAM Journal on Discrete Mathematics, 26(2):605–617, 2012.

  • [SSTW24] J. Sawada, J. Sears, A. Trautrim, and A. Williams. Concatenation trees: A framework for efficient universal cycle and de Bruijn sequence constructions. arXiv preprint arXiv:2308.12405, 2024.

  • [SW13] J. Sawada and A. Williams. A Gray code for fixed-density necklaces and Lyndon words in constant amortized time. Theoretical Computer Science, 502:46–54, 2013.

  • [SW23] J. Sawada and A. Williams. Constructing the first (and coolest) fixed-content universal cycle. Algorithmica, 85(6):1754–1785, Jun 2023.

  • [SWW13] J. Sawada, A. Williams, and D. Wong. Universal cycles for weight-range binary strings. In Combinatorial Algorithms: 24th International Workshop, IWOCA 2013, Rouen, France, July 10-12, 2013, Revised Selected Papers 24, pages 388–401. Springer, 2013.

  • [SBE+02] B. Stevens, P. Buskell, P. Ecimovic, C. Ivanescu, A. M. Malik, A. Savu, T. S. Vassilev, H. Verrall, B. Yang, and Z. Zhao. Solution of an outstanding conjecture: the non- existence of universal cycles with $k = n − 2$. Discrete Mathematics, 258(1):193–204, 2002.

Interested in generating other combinatorial objects? Visit http://combos.org