De Bruijn Sequence and Universal Cycle Constructions
| Random Generation | Output | ||||||||
|
A DB sequence of order $n$ is in one-to-one correspondence with an Euler cycle in the de Bruijn graph $G(n{-}1,k)$. Each Euler cycle corresponds to a unique rooted spanning in-tree (arborescence). By generating all such arborescences and considering all permutations for the remaining outgoing edges from each vertex, we can generate all Euler cycles (DB sequences). Furthermore, a DB sequence can be generated uniformly at random by generating a random arborescence and randomly ordering the remaining outgoing edges from each vertex. Similarly, we can generate universal cycles uniformly at random given the underlying Eulerian graph $H$ as follows (see Fleury's Euler cycle algorithm):
- Generate a random edge ($r,v$) in $H$, i.e., a string in $\mathbf{S}$, to obtain a random root vertex $r$
- Generate a random arborescence $T$ directed to root $r$
- Make each edge of $T$ (the bridges) the last edge on the adjacency list of the corresponding vertex, randomly assign the order of the remaining outgoing edges
- Starting from $r$, traverse the edges in $H$ (for $|\mathbf{S}|$ steps) by visiting the first unused edge in the current vertex's adjacency list
Since the graph $H$ is not necessarily regular, it is important to initialize the algorithm by selecting a random edge rather than a vertex. For Eulerian graphs, an arborescence can be generated uniformly at random by performing a simple random backwards walk until every vertex is visited. The first time a vertex is visited, the edge is recorded as a tree edge in the random arborescence [KMUW96]. The running time of the above algorithm depends on the cover time of the random walk, which is the number of steps it takes to visit every vertex. The algorithm has exponential time delay and requires exponential space. Experimental evidence of the cover time by applying this algorithm to the following objects is provided in [SG25].
DB sequences
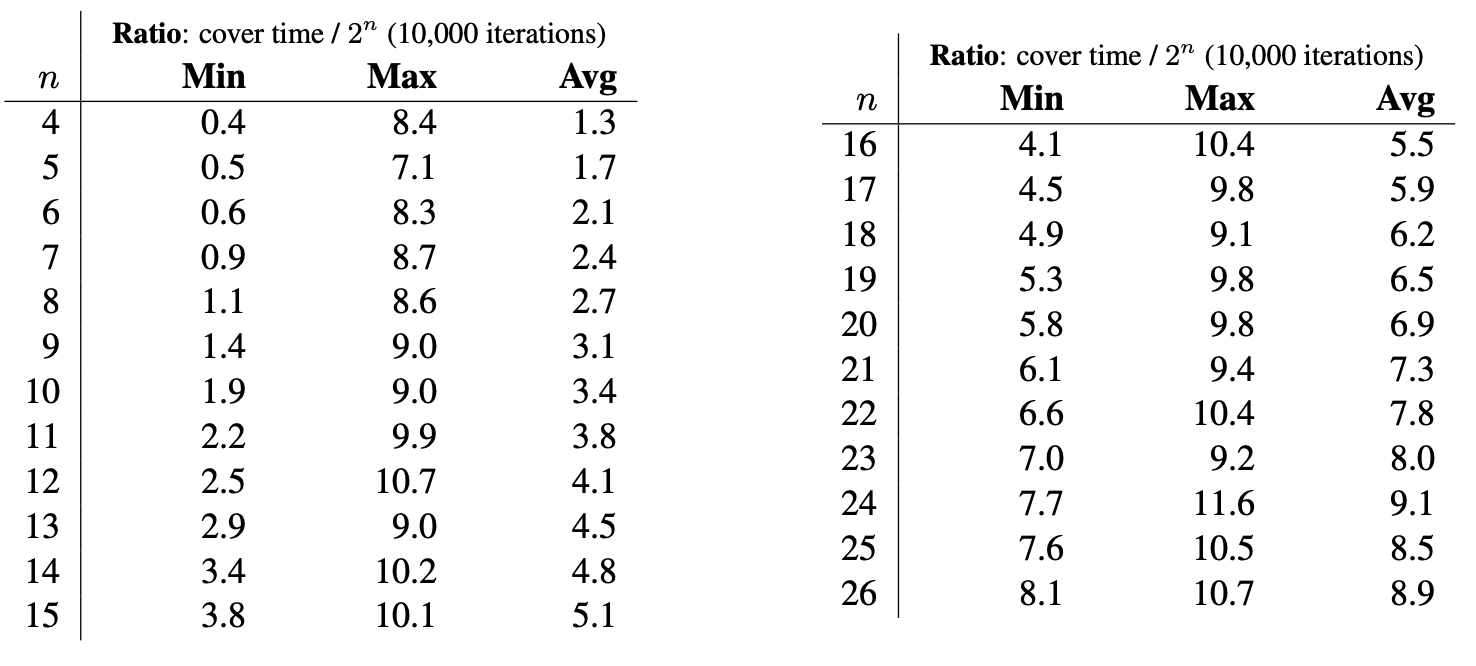
For DB sequences, the underlying de Bruijn graph $H = G(n{-}1,k)$ has $k^{n-1}$ vertices and $k^n$ edges. The following tables for $k=2$ illustrate the minimum, maximum, and average ratios of the cover time to total edges by running the random generation algorithm for 10,000 iterations.
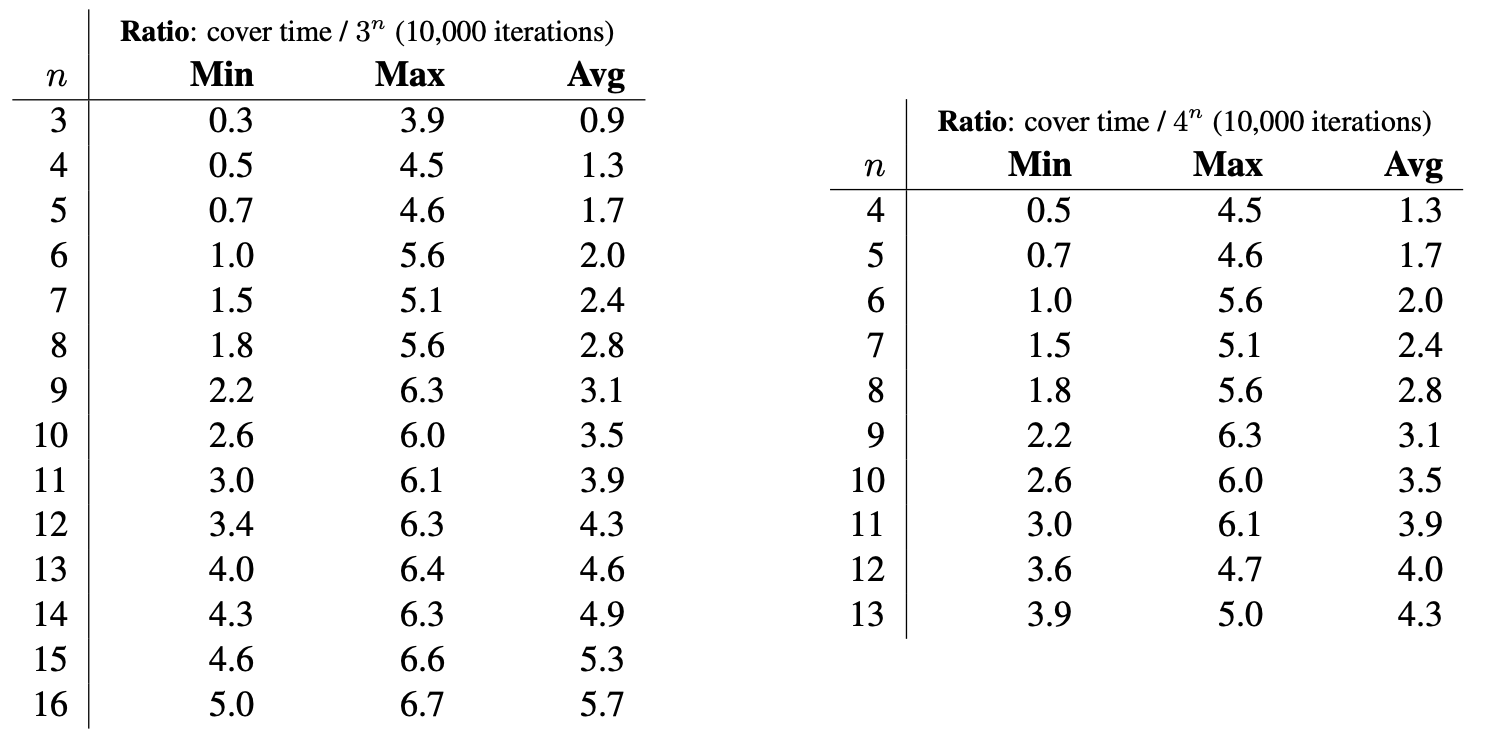
The following tables illustrate the same statistics for $k=3$ and $k=4$.
If an application does not require a sequence generated uniformly at random, an algorithm which applies a Burrows-Wheeler Transform can be applied; it outputs each DB sequence with positive probability [LP24]. The algorithm requires exponential space and has an exponent time delay with respect to the order $n$, but produces the sequence in $\alpha(n)$-amortized time per symbol for $k=2$, where $\alpha(n)$ is the inverse Ackerman function. The first estimate on the mean discrepancy of DB sequences is obtained using this algorithm [LP24].
Weight range DB sequences
A weight-range DB sequence is a UC for the set $\mathbf{S}_k(n,w_1,w_2)$ which contains all $k$-ary strings of length $n$ within a specified weight range. The underlying graph $H$ is not necessarily regular; a random edge can be generated by applying a straightforward recurrence.
Weight range DB sequences can be constructed efficiently via cycle-joining and an $O(n)$-time successor rule when the minimum weight is 0, or the maximum weight is $(k-1)^n$ [GSWW20]. In the binary case, they can be constructed for any weight range in $O(1)$-amortized time [SWW13]. Weight range DB sequences can be applied to construct universal cycles for subsets for two different representations.
DB sequences with forbidden $0^z$ substring
A DB sequence with forbidden $0^z$ is a maximum length UC that does not contain $0^z$ as a substring. The set $\mathbf{S}_k(n,z)$, which contains all length-$n$ strings over $\{0,1, \ldots, k{-}1\}$ that do not contain any cyclic string with $0^z$ substring, admits such a UC [CEN+24]. The underlying graph $H$ is not necessarily regular; a random edge can be generated by applying a straightforward recurrence.
The lexicographically smallest DB sequences with forbidden $0^z$ can be generated via a straightforward greedy algorithm [SWW16]; it can also be generated efficiently by concatenating the aperiodic prefixes of necklaces with no $0^z$ substring as they appear in lexicographic order [SWW16,GS18]. More such sequences can be efficiently generated by applying cycle-joining [CEN+24].
Permutations, subsets, and multiset permutations
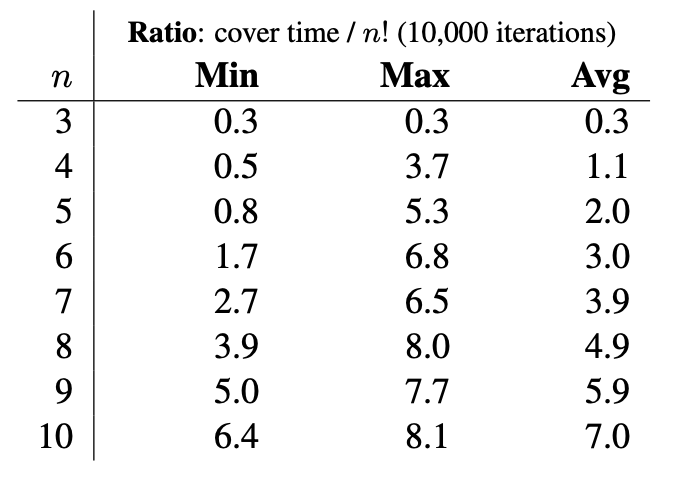
For shorthand permutations, the underlying graph $H$ has $n!$ edges. Each vertex has in-degree = out-degree = 2 and thus there are $n!/2$ vertices. A random permutation can easily be generated by applying the Fisher-Yates shuffle. The following tables illustrate the minimum, maximum, and average ratios of the cover time to total edges by running the random generation algorithm for 10,000 iterations.
For subsets represented by binary strings of length $n{-}1$ with either $k$ or $k{-}1$ ones (the last bit is redundant), the underlying graph $H$ has ${n \choose k}$ edges. Multiset permutations generalize both permutations and subsets.
A random permutation, subset, or multiset permutation can easily be generated by applying the Fisher-Yates shuffle. UCs for shorthand permutations, subsets, and multiset permutations, can all be efficiently constructed.
Weak orders
Let $W_n$ denote the number of weak orders with $n$ competitors. The number of weak orders where there is a $k$-way tie for first is given by ${n \choose k} W_{n-k}$. Thus, $W_n = \sum_{k=1}^n {n \choose k} W_{n-k}$. This recurrence can be applied to generate a weak order uniformly at random, which is required to select the root in the arborescence. See the corresponding enumeration sequence A000670 in the Online Encyclopedia of Integer Sequences.
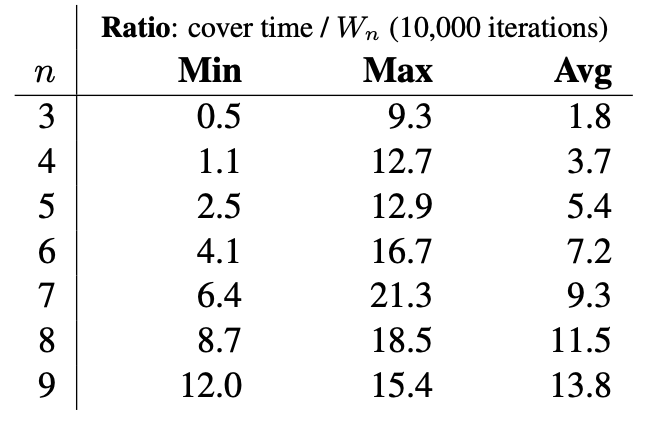
The following tables illustrate the minimum, maximum, and average ratios of the cover time to total edges by running the random generation algorithm for 10,000 iterations.
UCs for weak orders can be efficiently constructed.
Orientable sequences
Let $\mathbf{S}_k(n)$ denote the set of all strings corresponding to an asymmetric bracelet. A UC for $\mathbf{S}_k(n)$ is an orientable sequence with asymptotically optimal length. Consider the induced subgraph $H$ of the de Bruijn graph $G(n{-}1,k)$ where each vertex has an outgoing edge corresponding to a string in an asymmetric bracelet. The number of such edges, denoted by $S_k(n)$, has a known formula. To generate a random edge, we can randomly generate $k$-ary strings with rejection; on average only two random strings need to be generated as $n$ gets large.
The following tables illustrate the minimum, maximum, and average ratios of the cover time to total edges by running the random generation algorithm for 10,000 iterations.
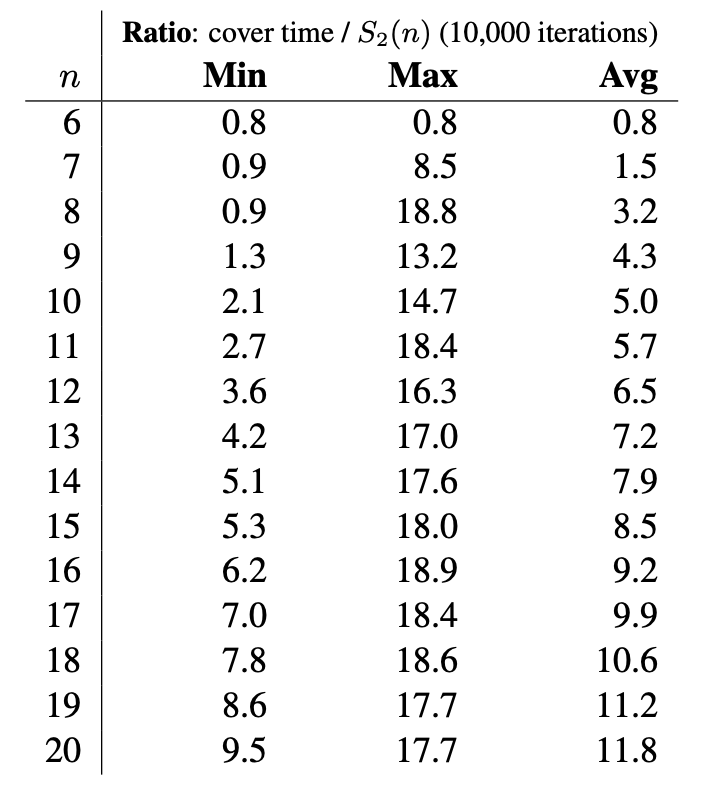
Orientable sequences with asymptotically optimal length can be efficiently constructed.
» (Non-uniform) DB sequence C++/Python
» Weight range DB sequence C program
» DB sequence with forbidden $0^z$ C program
» UC for shorthand permutations C program
» UC for shorthand subsets C program
» UC for shorthand multiset permutations C program
- [CEN+24] Y. M. Chee, T. Etzion, T. L. Nguyen, D. H. Ta, V. D. Tran, and V. K. Vu. Maximum length RLL sequences in de Bruijn graph, arXiv preprint arXiv:2403.01454, 2024.
- [GS18] D. Gabric and J. Sawada. Constructing de Bruijn sequences by concatenating smaller universal cycles. Theoret. Comput. Sci., 743:12–22, 2018.
- [GSWW20] D. Gabric, J. Sawada, A. Williams, and D. Wong. A successor rule framework for constructing $k$-ary de Bruijn sequences and universal cycles. IEEE Transactions on Information Theory, 66(1):679–687, 2020.
- [KMUW96] D. Kandel, Y. Matias, R. Unger, and P. Winkler. Shuffling biological sequences. Discrete Applied Mathematics, 71(1):171–185, 1996.
- [LP24] Z. Lipták and L. Parmigiani. A BWT-Based algorithm for random de Bruijn sequence construction. LATIN 2024: Theoretical Informatics, 130-145, 2024.
- [Rus03] F. Ruskey. Combinatorial generation. Working Version (1j-CSC 425/520), 2003.
- [SG25] J. Sawada, D. Gabric. Random generation of universal cycles and de Bruijn sequences. Submitted manuscript, 2025.
- [SWW13] J. Sawada, A. Williams, and D. Wong. Universal cycles for weight-range binary strings. In Combinatorial Algorithms: 24th International Workshop, IWOCA 2013, pages 388–401. Springer, 2013.
- [SWW16] J. Sawada, A. Williams, and D. Wong. Generalizing the classic greedy and necklace constructions of de Bruijn sequences and universal cycles. Electron. J. Combin., 23(1):Paper 1.24, 20, 2016.